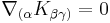Killing tensor
A Killing tensor, named after Wilhelm Killing, is a tensor, known in the theory of general relativity,  that satisfies
that satisfies
where the parentheses on the indices refer to the symmetric part.
This is a generalization of a Killing vector. While Killing vectors are associated with continuous symmetries (more precisely, differentiable), and hence very common, the concept of Killing tensor arises much less frequently. The Kerr solution is the most famous example of a manifold possessing a Killing tensor.